피아노 강좌
|
4. 음 정
|
▒ 음정
두 음간의 간격을 음정이라고 한다. 세는 단위는 도(degree)이며, 1도, 2도, 3도..등으로 음정을 나타낸다. C음과 겹쳐진 C 간의 음정은 1도이며, 도에서 이웃한 레는 2도, 미까지는 3도, 파까지는 4도... 이런 식으로 C(도) 와 한옥타브 높이에 위치한 C(도) 까지는 8도가 된다.
다음 그림은 C를 기준으로 쌓아진 음들이다. | |||||||||||||||||||||||||||
|
위에서 들어 본 소리들은 두 음의 동시 울림 소리이다. 여러 번 들어본 후 울림의 느낌을 비교해 보자. (오선위의 각 노트를 마우스 포인터로 클릭하면 해당하는 음들의 동시 울림 소리를 들을 수 있다.)
①, ④, ⑤, ⑧ 번의 소리들은 울림이 좋으며 이 음정을 각각 완전1도, 완전4도, 완전5도, 완전8도 라고 한다. 그 외의 ②, ③, ⑥, ⑦번은 각각 장2도, 장3도, 장6도, 장7도 이다. 다음 표는 각 음정에 포함된 반음의 갯수이다.
즉, 완전 1도는 같은 음이며 장 2도는 온음 1개로 이루어져 있고, 장 3도는 온음 2개, 완전 4도는 온음 2개와 반음 1개, 완전 5도는 온음 3개와 반음 1개, 장 6도는 온음 4개와 반음 1개, 장 7도는 온음 5개와 반음 1개. 완전 8도 즉 1옥타브는 온음 5개와 반음 2개로 이루어져있다. 이것은 모든 음악의 이론의 기초가 되므로, 만약 이것을 처음 접한다면 기억을 해 두는 것이 좋다. 이러한 음정들은 각 조(key) 에 따라 성질이 변한다. 즉, 임시표(샾, 더블 샾, 플랫, 더블 플랫) 에 의해 음간 간격이 넓어지거나 좁아질 수 있으며, 앞의 그림과는 달리 아래에 위치한 음이 미나 파에 오는 경우엔 각각 포함하는 반음의 개수도 달라지므로 당연히 그 성질이 변한다. | |||||||||||||||||||||||||||
|
완전 음정에서 반음의 개수가 하나 늘어날 경우에는 증음정이 되며, 반음의 개수가 감소 할 때는 감음정이 된다. 장음정에서는 반음의 개수가 하나 늘어날 경우 증음정, 감소할 경우엔 단음정이 되며, 하나 더 감소 할경우 감음정이 된다. 장음정에서 두개의 반음(=1온음)이 늘어나면 그것은 겹증음정이라 부른다.
참고로, 완전 3도라는 음정은 없으며, 마찬가지로 장4도라는 음정도 없다. 아래의 예제에서 음정을 다시 한번 정리 해 보자.  | |||||||||||||||||||||||||||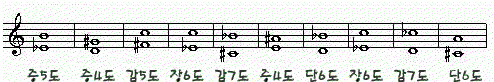
|
▒ 음정의 자리바꿈
음정을 만드는 2개의 음 중 아래의 음을 옥타브 위로, 또는 윗 음을 옥타브 밑으로 옮기는 것을 음정의 자리바꿈 이라고 한다.  위의 그림에서 처음 나오는 음정은 장3도이다. 이것을 자리바꿈하여 단6도가 되었다. 셋째 마디 그림의 음정은 완전 5도이며, 자리바꿈하여 완전 4도가 되었다. 마지막으로 증3도를 자리바꿈하여 감6도가 되었다. 이것을 잘 살펴보면 원래 음정과 자리바꿈 음정의 관계가 성립함을 알 수 있다. [ 9 - 원래음정 = 자리바꿈 음정 ] 단, 장음정을 자리바꿈하면 단음정이 되고, 단음정을 자리바꿈하면 장음정이 된다. 완전음정은 변함이 없으며, 증음정의 경우 자리바꿈 하면 감음정이 된다.
▒ 겹음정 (8도 이상의 음정) 1옥타브 밖의 음정을 겹음정이라고 한다. 보통은 12 ~ 13도 정도까지 세고, 그 이상 벌어진 음정은 자리바꿈 음정에서 센다. (9도 음정을 2도라고 해도 무방) 또한 한 옥타브 이내의 음정을 홑음정이라 한다.
예를 들어 C(도)음에서 12도 떨어진 음(솔) 을 12도, 또는 완전 5도 음정이라고 볼 수 있다.
| |||||||||||||||||||||||||||
P(perfect)는 완전음정의 약자이다. P4, P5등.. 또한 장음정은 Major의 약자인 M으로 표기하고 단음정은 Minor의 약자인 소문자 m 으로 표기한다. M6, m3 등..
